コンピューターのスピードとパワーが増すにつれ、何にでも数値計算を使いたくなります。私は古い人間なので、数分考えるだけで、コンピューターで何時間も浪費せずに済むような計算をいつも楽しんでいます。
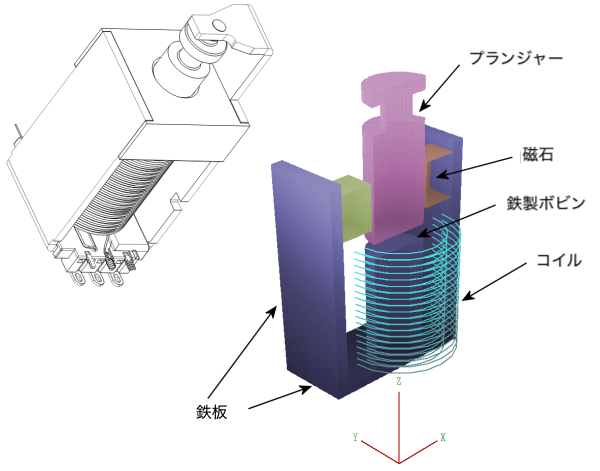
最近、あるメーカーから、ラッチング・ソレノイドの力を特性評価するためにMagnumを使用する方法を示すデモの作成を依頼されました。図1はソレノイドアセンブリの図面とMetaMeshで作成したメッシュです。
ネオジム鉄永久磁石はプランジャーの方向に磁化されています。この永久磁石は、プランジャーをスチールボビンに接触させるための静止保持力を与えます。
電流の極性によって、コイルは永久磁石に対抗してソレノイドのラッチを解除したり、永久磁石を補助してプランジャーを引き寄せたりします。
図1. ラッチングソレノイドの形状
プランジャーがボビンから分離している場合、力の計算は容易でした。この場合、プランジャーは空気（μr = 1.0）の要素に囲まれていました。ここではMagViewのSurface integralコマンドを使用しました。設定ファイルmagview_standard.cfgにより、積分はマクスウェル応力テンソルから決定された力の成分を与えました。
このメーカーは、ラッチ状態（すなわち、コイル電流がない状態でプランジャーがボビンに触れている状態）の保持力に特に興味を持っていました。この場合、プランジャーとボビンは実質的に同じ材料であるため、プランジャー周りのマクスウェル積分は適用できませんでした。数値的に考えて、私の最初のアイデアは、幅dgが小さくなるエアギャップで一連の計算を行うことでした。その意図は、力の変化をギャップゼロまで外挿できる補間関数でフィッティングすることでした。
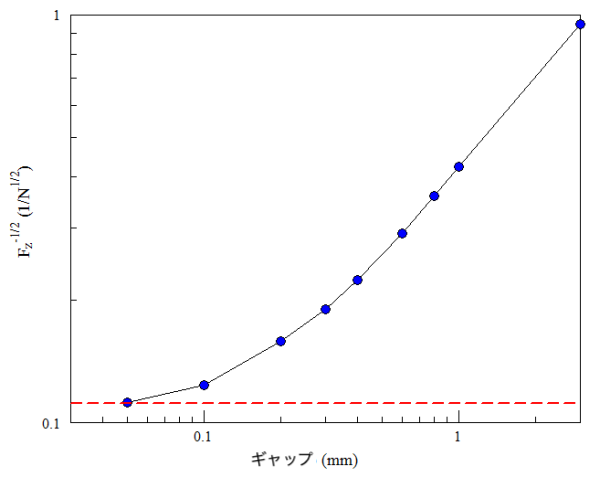
次の図の青い点は、計算結果の一部を示しています。Fz対dgの単純なプロットは、力が分離範囲にわたって2桁も変化したため、特に参考にはなりませんでした。この強い変動は、2つの磁石が近づくとピタリとくっつくというおなじみの経験を反映しています。ギャップが0.5 mmを超えると、力は～1/dg2のように変化することがわかりました。そこで、Fz-1/2対dgの対数プロット図を作成しました。このプロットは、力がゼロ間隔で一定値になる傾向があることを示しています。このアプローチは、労力の面でも数値精度の面でも効果的ではありませんでした。一定値への変曲点を観察するためには、非常に小さなギャップ幅（dg ＝ 0.05 mm）を使用する必要がありました。計算されたポイントへの多項式フィットには、大きな誤差がありました。
図2. ギャップ幅の関数としてのスケーリングされた力の変化。
幸いなことに、dg=0.0 mmのときの磁束分布の知識から正確な保持力を決定する、より簡単な方法を発見しました。プランジャーをボビンから無限小の距離dxだけずらしたとします。エアギャップ内の磁場は、ゼロギャップ磁場B0にほぼ等しい値で、スチール部品の断面積Aに閉じ込められたままとなります。磁石回路の磁場エネルギーの変化は
dU ≅ (B02/2 μ0) A dx.
仮想仕事の原理を用いると、保持力は
Fz = – dU/dx = – (B02/2 μ0) A
プランジャー直径が10.0 mmの場合、面積はA = 7.854 × 102 mm2でした。Magnumの計算では、平均磁束密度B0 = 1.61 Tとなり、Fz = -80.935 N（図2に赤破線でプロット）の総力が得られました。質量当量は8.25 kGでした。プランジャーとボビンの表面接触の精度に力が敏感に依存するため、この値は最大値でした。わずかな隙間でも大きな減少をもたらします。比較のため、メーカーは6〜7 kGの範囲の値を測定しました。
この計算は、数値計算と分析的手法を組み合わせることがいかに大切かを示しています。このケースでは、ギャップがゼロのときの磁束密度分布B0を求めるために数値計算が必要でした。一方、解析的な洞察は、保持力を決定するための文字通りの数値的アプローチよりもはるかに効果的でした。
