静電場数値解析（シミュレーション）における誘電体と導体の組み合わせ

EStatとHiPhiは、理想的な誘電体や理想的な導体の集まりの静電場を求めることができます。誘電体のように作用する材料と、導体のように作用する材料もあるような計算の扱い方について、よく質問を受けます。EStatとHiPhiのマニュアルには簡単なガイドラインがあります。この投稿では、基礎となる理論と解法について、より完全な説明をしたいと思います。

まず定義から始めましょう。理想的な誘電体とは、ルーサイト、テフロン、アルミナのような、実質的に無限大の抵抗率を持つ材料のことです。長い電圧パルスであっても、実電流の伝導を無視することができます。もう一方の極端にあるのが理想的な導体です。ここでは、実電流の流れは変位電流の流れよりもはるかに大きくなります。Δtを電圧パルス長とすると、実電流が支配的であるための条件は次のように書けます：

Δt ≫ εr ε0/σ、

ここで、εrは比誘電率、σは導電率です。(静電場解析の場合、σがゼロでないすべての材料における電圧分布は、実電流の流れによって決まります。

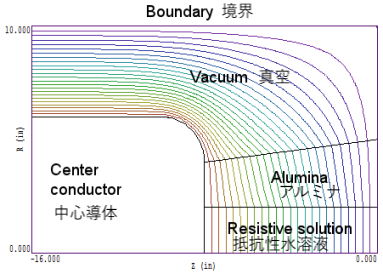
解決策を例で説明するのが一番わかりやすいでしょう。下の図は、パルスパワー電源をテストするためのダミー抵抗負荷です。このシステムは円筒対称であり、底辺に沿ったz軸に関して回転対称な図となっています。外側の境界は接地電位です。高電圧電極は、アルミナの中に満たされた硫酸銅の水溶液からなる抵抗器に接続されています。水溶液の導電率は、電圧パルス長に関する上式を満たすのに十分高いと仮定します。この状況では、水溶液は理想的な導体のように働き、他の材料（アルミナと真空）は理想的な誘電体です。

この計算方法は、2つの観察から導かれます：

水中の電圧分布は実電流の流れによって決まり、周囲の構造物の電圧分布とは無関係である。
水と絶縁体の境界では、実電流の平行成分のみが存在する。j = σEなので、境界における電界の法線成分はゼロである。
誘電型の解法（dielectric-type solution）を行い、水領域の比誘電率を周囲の絶縁体の比誘電率よりはるかに大きな値にすれば、この2つの条件を満たすことができます。