物理的な直感は、平均すると半分の時間では役に立ち、残りの半分の時間では誤解を引き起こします。その一例として、あるトライアルユーザーがMagnumをテストするために、最も基本的だと思われる磁石の問題を設定しました。プログラムは、彼の予想と約5倍も異なる結果を返しました。彼は自分の計算の何が間違っているのかを見つけるために私に連絡してきました。結論から言うと、彼の設定は完璧に正しく、プログラムも正しい答えを返していました。彼の予想が間違っていたのです。
磁気回路の概念は、実験室用マグネット(鉄磁束導体、小さなエアギャップ、駆動コイルを持つシステム)で達成可能な磁束密度を見積もるのによく役立ちます。この理論は、拙著『Principles of Charged Particle Acceleration(荷電粒子加速の原理)』(cpa.htmlから無料でダウンロード可能)の5.7節で取り上げています。この関係はアンペールの法則と磁束保存則から導かれます。永久磁石で駆動する回路では、この問題は曖昧になってきます。実際、拙著の5.8節は誤解を招きやすいと認めざるを得ません。現実には、永久磁石回路のギャップ磁界は、アセンブリの組み立て方に依存します。
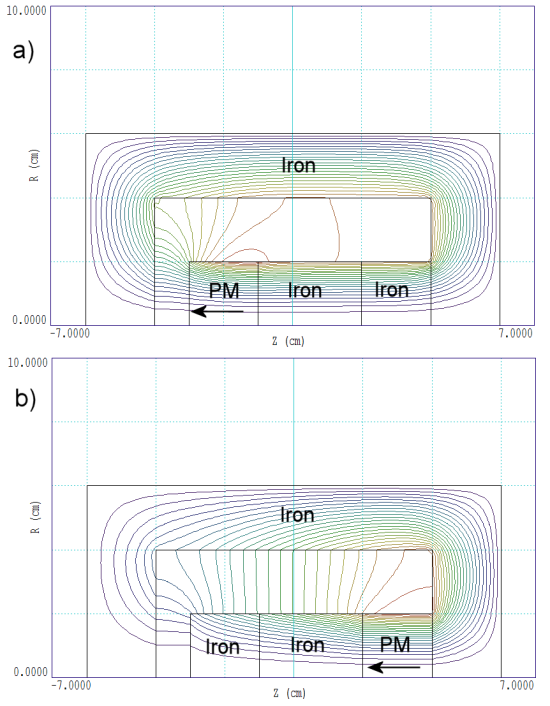
図1. 永久磁石回路のPerMagによる計算
この問題は、例を挙げるとよく理解できます。図1は、PerMag計算用の円筒形磁気回路を示しています。エアギャップと永久磁石は半径2.0cmの円筒形です。ギャップの長さはLg = 1.0 cmで、磁気の長さはLm = 2.0 cmです。理想的な永久磁石はBr = 1.0テスラで、鉄はμr = 500です。磁気回路の直感的な見方は、Bの線が高抵抗の鉄の中を強制的に流れる(すなわち、鉄が磁気導体である)というものです。この場合、回路の挙動は永久磁石の相対位置に依存しないはずであり、図1に示した2つの形状について同じギャップ磁場が予想されます。磁束を含むという仮定の下で、5.8節の理論は平均ギャップ磁場を予測する:
Bg = Br/(1 + Lg/Lm)
計算のパラメータでは、式はBg=0.67テスラを意味します。
PerMagの計算では、ケースaのギャップ磁場は約Bg=0.57テスラでした。この結果は、漏れ磁束とフリンジ磁束による磁束損失を考慮すれば、理論と一致します。一方、下図の配置のギャップ磁場はわずか0.15テスラであり、大きな差があります。磁束密度Bの磁束線が鉄によって「封じ込められる」という考えは明らかに間違っています。磁束線の性質をもっとよく理解する必要があります。
永久磁石の左側から出ている磁束密度の線は、できるだけ簡単な方法(すなわち、最もリラクタンスの小さい経路)で右側への道を見つけようとします。aの場合、磁束線はエアギャップに直接現れます。短いギャップを横切り、鉄を通って戻ってきます。一部の線は、外側の鉄片に近道するか、空気を通って磁石の上流側に直接戻ります。
対照的に、ケースbのB線は、エアギャップに到達する前に、鉄を通って比較的長い距離を移動しなければなりません。内側鉄片と外側鉄片の間のラジアル・ギャップのリラクタンスは、ワーキング・ギャップのそれよりも小さくなります。その結果、磁束線は早期に切断され、磁束の大部分はワーキング・ギャップに到達しません。この例は、実用上重要な意味を持ちます。永久磁石回路のエアギャップ内で最大の磁束を発生させることが目的であれば、磁石はギャップに隣接させるべきです。










