私たちの荷電粒子解析コードTrakとOmniTrakは、システムの全体サイズと比較して点とみなすことができる荷電粒子(例えば、電子、イオンなど)にかかる力と粒子軌道を計算します。今回は、有限サイズの中性誘電体粒子や金属粒子上の電気力を求める方法について説明します。思い浮かぶ応用例は、電気集塵装置内の小さな誘電体上の力です。ここでは、強い勾配を持つ電場が物体上の電荷分布の分極を引き起こします。この力は高電界側の電荷に強く働くため、物体を高電界領域に引き寄せる正味の力が生じます。これは2次的効果であるため、結果として生じる力は非常に小さくなる可能性があります。課題は、十分な精度で数値計算を構築することです。大域的な電場分布を求めなければなりませんが、小さな物体を表現するのに十分なメッシュ分解能を維持しなければなりません。この投稿では、HiPhiを使った例を紹介します。以下のコード機能により、このアプリケーションは実現可能です:
・マクスウェル応力テンソルの自動表面積分を行い、物体にかかる正味の力を求める。
・応力テンソル積分の精度を向上させるために、対象物の周囲に診断面を定義する。
・BOUNDARYテクニックを使用して、小さな要素を使用しながら短い実行時間を維持します。
HiPhiを使った計算をご覧になりたい方は、以下のリンクから例題ファイル一式をダウンロードしてください:
precipitator01.min
precipitator02.min
precipitator03.min
precipitator01.hin
precipitator02.hin
precipitator03.hin
precipitator.scr
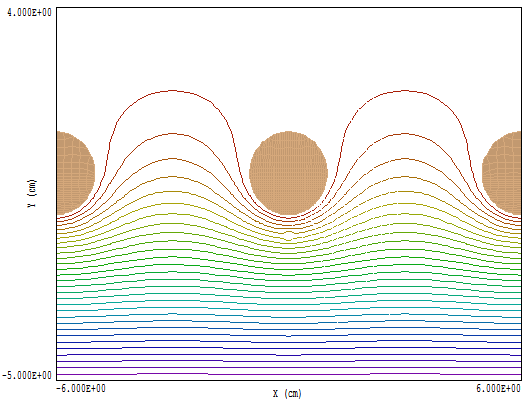
下の最初の図は、計算された等ポテンシャル線の全体図です。50kVのロッドのアレイと下部の接地面は、電界勾配を作り出しています。左右には対称境界があります。物体は直径2.0 mm、εr = 5.6の誘電体球で、中心棒の1.5 cm下に位置しています。対応する場の擾乱が最初の図に見えます。
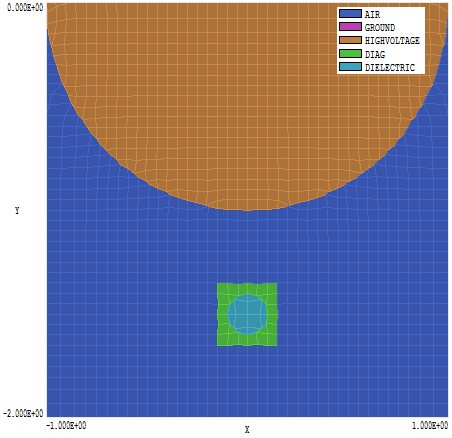
2番目の図は、物体近傍のメッシュの詳細です。球は辺3.0 mm、εr = 1.0の立方体に囲まれています。この領域の機能は、マクスウェル応力テンソルを評価するための第2の表面を定義することです。理論的には、球と箱の積分は同じ結果を与えるはずですが、実際には、電場はボックス形状上でより滑らかな変化を持つので、より良い推定が期待できます。この設定には2つの問題があります:
物体近傍のメッシュは全体計算では比較的粗くなり、実行時間が短くなります。表面積分の精度はあまり期待できません。
診断ボックスの大きさを検討する必要があります。表面は、球によって生成される場の変化の領域内で、比較的近くにあるべきです。表面が遠すぎると、球のわずかな効果が数値ノイズに埋もれてしまいます。
以下は、球に沿う力(リージョン4)と球と診断ボックスのアセンブリ(リージョン4と5)を求める解析スクリプトの内容です:
OUTPUT Precipitator01 INPUT Precipitator01.HOU FORCE 5 FORCE 4 5 ENDFILE
Maxwellルーチンは、理論値1.2566E-5 m2に対し、1.2382E-05 m2の表面積を返しました。この差は、球面形状のファセット近似を反映しています。計算された力は、球面ではFy = 2.9902E-06 N、診断面ではFy = 5.1111E-06 Nでした。この大きな差は、粗いメッシュでの不正確な電場の補間によるものです。球面に対してεr = 1.0で計算を繰り返すことで精度を測ることができます。原理的には、力はゼロになるはずです。この場合、診断上の積分はFy = -7.0565E-07となります。従って、箱の表面積分は〜10-20%の誤差があると予想されます。
HiPhiの便利な機能は、ディリクレ境界条件を設定するための大域解(全体の計算)を使って微視的解(局所的な計算)を構築できることです。今回は、誘電体を中心とした一辺が2.0cmの立方体の箱の中で微視的解を作ってみました。下の3番目の図は、要素サイズ0.2 mmの場合、平面z = 0.0 cmの等ポテンシャル線の計算結果です。この場合、球の計算表面積は理論値に近い1.2637E-05 m2です。計算された力は、Fy = 5.7093E-06 N(球)とFy = 6.9591E-06 N(診断ボックス)です。球体のεr = 1.0では、箱の力の差はFy = -8.5519E-08 Nとなり、計算値の約1.2%に過ぎません。従って私は6.96E-6 Nという値が正解に近いと予想しています。もしこの数値に命が懸かっているとしたら、箱の近くの要素を小さくして計算を繰り返してもよいでしょう。
どのような計算においても、設定に誤りがあった可能性を常に考慮しなければいけません。数値結果が妥当かどうかをチェックするのは良い習慣です。別の方法として、仮想仕事法を使うことができます。指定された電圧を持つ静電システムにおいて、物体を距離Δdだけ変位させ、全電界エネルギーΔWの変化を観測すると、変位方向に沿った力成分はF=ΔW/Δdとなります。この方法を適用するために、球と診断ボックスをy方向に+1.0mm変位させた2番目の微視的解を作りました。PhiViewのFull解析機能を使い、全体領域の場のエネルギー5.86829E-05 Jを求めました。差の8.1E-9 Jを0.001で割ると、垂直方向の力の推定値Fy = +8.1E-6となり、大体予想の範囲内です。エネルギー法は数値間の極めて小さな差に依存するため、高い精度は期待できないでしょう。仮想仕事法のもう一つの欠点は、2つの計算を必要とすることです。