有限要素法数値解析ソフトAMaze/TriCompのコードパッケージは広範な機能を持ち、難しい物理の計算に挑みます。午後の時間を使ってボタンを押せば、誰でもパッケージを習得できると考えるのは非現実的でしょう。一方、コードは大きいとはいえ、あなたの理解やコントロールを超える必要があるのでしょうか?完全な信頼を必要とする、近寄りがたいブラックボックスなのでしょうか?
この記事の目的は、そうではないことを示し、プログラムを手なずけるためのステップを説明することです。その戦略とは、私たちが行っているのと同じような手順を踏むことです。
私たちが3D計算コードを完成させるとき、これほど複雑なものが正しい答えを出すとはとても考えられないように思えます。そこで私たちは、シンプルで議論の余地のない計算からテストを開始します。そこで発生した問題を特定し、修正し、正しい答えが得られることを確認し、そしてまた次の少し複雑にした段階へと進みます。
あなた自身の解析対象の計算設定を作る準備ができたら、答えがわかっている単純な構造から始めてください。結果が自分の期待にそぐわない場合は、その原因を突き止めましょう。いくつかの例を見れば、プログラムについて、また一般的な数値テクニックの限界について多くを学ぶことができるでしょう。説明のために、HiPhiを使って静電場計算のテストを行い、答えを教科書の結果と比較します。その過程で、数値計算の正確さをチェックし、静電容量の計算を復習します。
下図は、理想的な球形コンデンサの形状を示しており、外側電極はr0 = 5.0 cm、内側電極はri = 2.0 cm、間にεr = 2.7の誘電体があります。要素幅は約0.2cm。クローズドシステムにより、有限要素法では避けられない境界の問題を避けることができます。メッシュは、MetaMeshで、解析領域を外壁で満たし、誘電体の球体部分を切り出し、すべての共有節点が外壁に関連するように外表面をコーティングし、次に内側の球体を追加することによって作成します。内側電極の電位はV0 = +1.0Vで、外側表面は接地されています。要素サイズが比較的大きいため、HiPhi計算にかかる時間はわずか15秒です。
ファイル”sphere.scr”はPhiView用の解析スクリプトで、次のような内容です:
* File SPHERICAL_CAPACITOR.SCR * Copyright, Field Precision, 2008 OUTPUT Spherical_Capacitor INPUT Spherical_Capacitor.HOU * Check absolute values at two points * 2点の絶対値をチェックする POINT 3.0 0.0 0.0 POINT 4.0 0.0 0.0 * Calculate global field energy to find capacitance * キャパシタンスを求めるための全体エネルギーの計算 FULLANALYSIS * Determine induced charge and compare capacitance values * 誘導電荷を決定し、キャパシタンス値を比較する。 REGION 1 REGION 3 ENDFILE
予測される電極間の電界の変化は以下の通りです:
Er(r) = (V0/(1/ri – 1/ro)
ここで、すべての量はSI単位です。以下は2点でのコード結果です:
Radius Er(analytic) Er(code) Difference (cm) (V/m) (V/m) ================================================ 0.03 37.037 37.186 0.402% 0.04 20.833 20.850 0.082%
絶対値の一致が非常に良いのは気持ちの良いものです。どんな数値計算でもそうですが、一致度は完全ではありません。MINファイルの要素サイズを0.1cmに小さくすることで精度を向上させることができます。その代償として、実行時間は8倍以上になります。どのような数値計算においても、必要な精度を決定し、余裕のある実行時間とのバランスを取る必要があります。
同心球間のキャパシタンスの式は次の通りです。
C = 4π εrε0/(1/ri – 1/ro)
この場合、予測値はC = 1.0014 × 10-11 Fです。PhiViewで2電極システムのキャパシタンスを求めるには2つの方法があります:
1) 全体の電界エネルギーを求め、U = CV2/2 の式を使用するか、2) 電界の法線成分を計算して電極表面の電荷を求めます。
したがって、静電容量はC = 9.9423 × 10-12 Fとなり、理想値より約0.72%低くなります。この差の主な原因は、内部電極の体積の差でしょう。繰り返しになりますが、要素サイズを小さくすれば、結果はかなり改善します。
誘導電荷の計算では、内側電極で-1.02134×10-11クーロン、外側電極で1.00928×10-11クーロンとなります。誘導キャパシタンス値は、理論値から内側で+2.1%、外側で+0.93%異なります。
誘導法は、媒体を介した平均的な補間ではなく、電極に近い局所的な電界の補間を含むため、一般にエネルギー法よりも精度が低くなります。外側電極の方が精度が高いのは、表面のファセット数が多く、球に近いからです。
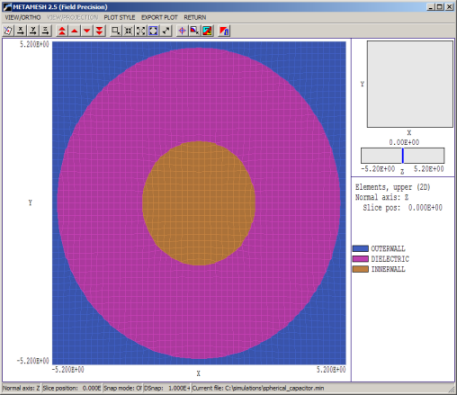
同心球の静電容量。
- Field Precision home page: www.fieldp.com.










