シートビーム電子入射装置は、産業用加工に長い間使用されてきました。このような用途のデバイスは一般に、断面積が大きく、電流密度が比較的低く、ビーム品質に対する要求が最小です。その開発は主に経験則によって行われてきました。最近、革新的な高周波、高出力マイクロ波源を駆動するためのシート状電子ビームに大きな関心が集まっています。このような応用では、電子のダイナミクスが空間電荷効果に強く影響されるレベルの電流値で、強く集束されたビームが必要とされます。三次元の空間電荷が支配的な入射器に関する広範な研究の結果、洗練された設計が生み出されました。
この記事では、高品質のシートビームを作る簡単な方法について述べます。この方法は、非常に高いアスペクト比(すなわちRy/Rx ≫ 1.0)の楕円ビームを作ります。この方法は、中程度から低パービアンスの限界の空間電荷が支配的なビームに適用されます:
P = I/V^1.5 < 1.0E-6
式中、I はビーム電流(アンペア)、V は入射器電位(ボルト)です。この式は、加速ギャップの幅dがビームの直径に比べて大きいことを意味しています。
シートビームのコンセプトを理解するためには、円形ビーム銃の基本を復習する必要があります。円形ビーム用の中程度のペービアンスの入射器を設計するためのガイドラインは、私の著書Charged Particle Beams (Wiley-Intersience, New York 1990)の7.1と7.2節で述べられています。この本は https://www.fieldp.com/cpb.html からダウンロード可能です。この戦略は、加速ギャップに収束するビームを生成するために、形状の整ったカソードと集束電極を使用することです。アノード取り出し開口部の直径を小さくすることで、ギャップ電界への影響を最小限に抑えることを意図しています。アパーチャ近傍の横電界はビームをデフォーカスさせます。円形絞りは負の焦点距離を持つレンズのように作用し、f = -4dで近似的に与えられます。この式の導出は、拙著 “Principles of Charged Particle Acceleration” (Wiley, New York, 1986)の6.5節に記載されており、http://www.fieldp.com/cpa.html からダウンロード可能です。ギャップの収束の度合いに応じて、アパーチャーから取り出されるビームは発散するか収束するかのどちらかになります。
図1は、パラメータV = 20.0 kV、I = 0.46 A、P = 0.16 μpervの円形ガンの設計(当社の2次元コードTrakで作成)を示しています。カソードは、曲率半径25.0mm、外半径2.0mmの球形断面です。平均電流密度は約3.8A/cm2、 集光電極の形状は、1)カソード上の空間電荷制限電流密度がほぼ均一であること、2)取り出されたビームのエミッタンスが低いこと、を保証するために試行錯誤の調整によって決定されました。図の電極形状では、アパーチャーの出口で平行ビームが得られます。電子の方向の誤差は0.1°以下です。
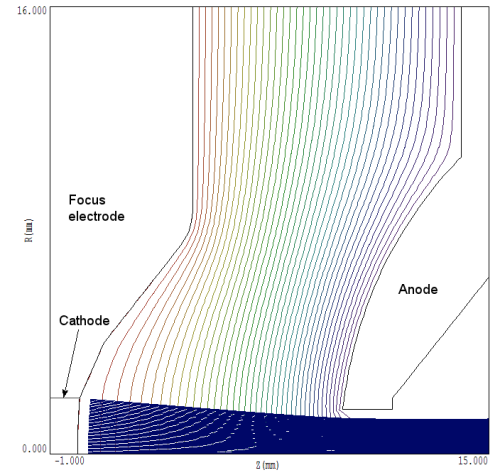
図1. 0.16 μpervの円形ビーム入射器のモデル電子軌道と静電ポテンシャル線。
円形インジェクタの設計を考えると、ラインフォーカスを生成する最も簡単なアプローチは、円形アパーチャをスロットに置き換えることです。スロットがx方向に実質的に無限の長さを持つ場合、2つの変化があります:
・開口部に近いx方向の横力は小さくなります。
・y方向の力は2倍になり、スロットアパーチャーの焦点距離はおよそf = 2dになります。
その結果、ビームはx方向に収束し、y方向に拡大します。x方向の焦点では、Ry > Rxのほぼ楕円のビームが観測されると予想されます。主な問題は、印加電界とビーム生成電界の変動によって決まる最小焦点スポットの限界です。
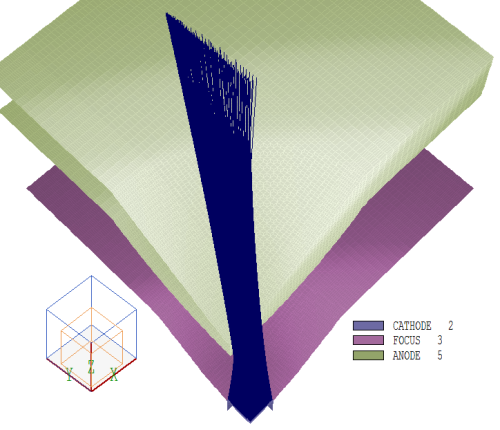
3次元のOmniTrakコードを使用すれば、数値的に厳密な解を求めることができます。図2にその形状を示します。カソード、集束電極、アノードは、2次元の計算と同じ形状の回転体です。唯一の違いは、陽極を貫通する高さ3.0 mmのスロットをx方向に切っていることです。このコードでは、正味電流は0.437 Aとなり、2次元の結果に近くなりました。予想通り、低パワーの銃ではアパーチャーの形状は比較的小さな影響しか及ぼしません。焦点はz = 36.4mmの位置(カソード中心に対して)にできます。
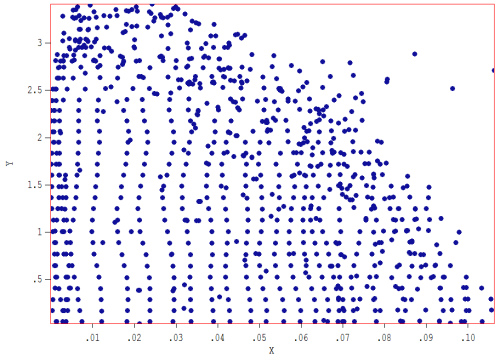
図3は、クリティカルデータである短焦点でのビームプロファイルを示しています。プロファイルはほぼ楕円です。長半径はRy ≅ 3.4 mmですが、短半径はRx ≅ 0.106 mmしかありません。この形状により、ビームスポットのアスペクト比Ry/Rx ≅ 32のタイトな短方向フォーカスが得られます。短方向焦点では、ビームはy方向に小さな角度広がりを持ち、包絡線発散角は約6°です。短距離方向の二乗平均発散角は1°未満です。アスペクト比と焦点位置の変更に関しては、2つの自由パラメータがあります:
すべての寸法は、パービアンスを変えることなく、係数で拡大縮小することができます。
加速ギャップの収束角度を変更することができます。
2つ目のオプションに関しては、コンバージェンスを高くすると、焦点位置がアパーチャーの出口に近づきます。同時に、yにおける包絡線拡大角は減少します。したがって、銃のコンバージェンスはRy/Rxに強く影響します。