薄いシートは有限要素計算にとって悩みの種です。スケールに大きなばらつきがあると、悪いメッシュや悪い結果につながります。この問題は、光電子増倍管のような高感度機器の周囲の磁場レベルを下げるために鉄やミューメタルの薄い層を使用する磁気シールド計算でしばしば発生します。このような場合、文字通りのアプローチではなく、スケーリング原理を採用するのが有効です。メッシュの作成に頭を悩ませることもなく、精度もよくなることが多いのです。
説明のために、J.D. Jackson, Classical Electrodynamicsにある、一様磁場に浸された中空の鉄球の例を使います。図1はこの形状をr-z座標でプロットしたものです。(この図は球の半分を示しているのではないことに注意 – 球全体をrとz座標で示しています)。球は外半径roと内半径riを持っています。比透磁率μrの鉄のような物質でできています。球から遠い磁場は一様な値Bz = Boです。解析解は、μr ≫ 1ならば、内部の磁場は一様で軸方向であることを示しています。球内部の場と遠方の場の比は
Bi/Bo = (9/2*μr)/(1 – ri^3/ro^3) [1]
です。
球の厚さが平均半径に比べて小さいと仮定し、Δr = r0 – riをとり、二項展開すると、比は次のように書けます:
Bi/Bo = (3*ro)/(2*μr*Δr). [2]
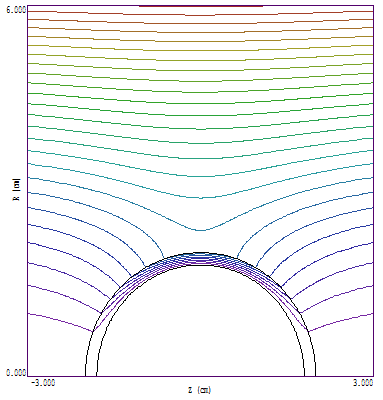
図1 一様磁場中の中空鉄球
この結果を確認するために、円筒対称のPerMag解析を実行することができます。半径ro = 2.0cmの球を、半径10.0cm、長さ20.0cmの円柱という大きな計算領域の中に置きます。球のないところに一様な磁場Bz = 0.050テスラ(500G)があるように設定します。この場合次のようなトリックを使います:
左と右の境界は、PerMagの自然境界条件であるノイマン条件(垂直な磁場)にします。
軸上のベクトルポテンシャルをr*Aθ = 0.0に設定します(ディリクレ条件)。
Rの外側の境界上のベクトルポテンシャルをrAθ = Bo*R^2/2 = 2.5E-4(ディリクレ条件)とします。
鉄をμr = 1.0に設定して最初の計算を行い、このテクニックを確認してみます。
最初の計算では、球の内半径はri = 1.95 cmで、厚さ0.05 cmに相当します。シェルを表現するために、0.025cmの小さな局所要素サイズを使用します。この計算では、計算された内部磁場は1.187E-3テスラで、理論予測の1.200E-3テスラに近い値になっています。
2次元PerMagコードで非常に小さな要素を使用するのは比較的簡単ですが、3次元Magnumコードで薄いシェルをモデル化するのはかなり困難で時間がかかります。別の方法として、式2がμr*Δrの積を含むことに注目します。シェルの厚さを2倍にし、μrの値を半分にしたらどうなるでしょうか?Δr≪riである限り、ほぼ同じ答えが得られるはずです。言い換えれば、スケーリング関係を適用することで解を単純化しているのであり、コンピュータ以前の工学ではおなじみのアプローチです。厚さΔr=0.10cm、μr=1250とすると、シールド内部の計算電界は1.218E-3テスラになります。厚さΔr=0.15cm、μr=833.3の場合は1.2492E-3テスラとなり、約4%の誤差が生じます。
一般的なルールとして、2Dまたは3Dの磁気シールド計算では、実際のシートと調整したシートの厚さがシールドされるボリュームのスケールサイズに比べて小さい限り、μrを小さくした厚いシートで代用することができます。シールドの一部が飽和すると、この手順は無効になることに注意が必要です。この条件は、スケーリング関係の基礎となる直線性の仮定に反します。関連する質問として、シールドが飽和しているかどうかをどうやって知るかということがあります。μrの妥当な固定値で計算を行い、材料のかなりの体積にわたってBが飽和値Bsを超えるかどうかをチェックしてください。鉄の飽和磁場はBs=2テスラ程度で、ミューメタルのような材料ではもっと低くなります。
Permagの例を実行したい場合は、ここに入力ファイルへのリンクがあります:










