有限要素静電場解析は、有限の解析領域に適用されます。EStatとHiPhiの新規ユーザーが直面する最も一般的な問題の1つは、解析領域の境界をどのように扱うかです。課題は、物理系を最適に表現するために境界の特性を設定することです。
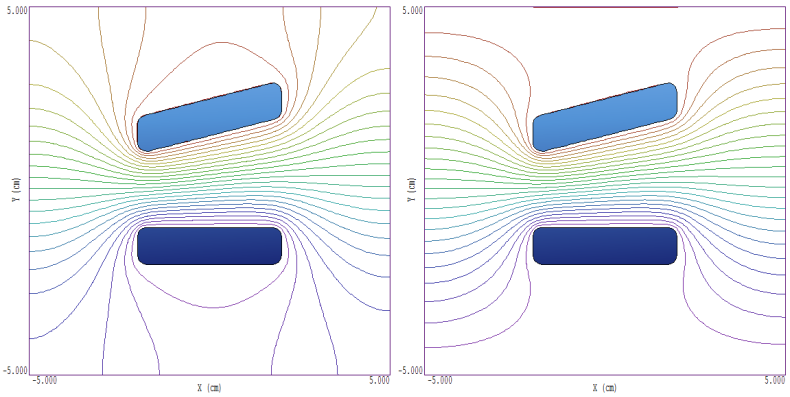
図1. 境界条件の選択を変えた場合の静電場。
図1に示すような2つの電極から発生する場を考えてみましょう。電極にしか興味がないから、境界は何もしない」と言うのが最初の発想かもしれません。この場合、境界は特殊なノイマン条件を仮定しており、有限要素解法では自然な境界条件です。左図のように、等電位の等高線は境界に垂直であり、電界は平行です。この解析結果について何が言えるでしょうか。
- 延長されたノイマン境界は、解の収束を遅らせます。これはHiPhiで特に懸念されることです。
- 境界は等高線を強制的に垂直にするため、電極付近の領域は無限の自由空間中のように振舞うことはありません。その代わり、解はx方向にもy方向にもの無限の電極ペアが存在する場合に対応します。
- 電界の線は角で直角に曲がるので、解は完全に物理的なものではありません。
完全な解の定義のためには、2つのことを考慮する必要があります: 1)主な関心領域と、2)解析領域の周囲の環境です。この場合、関心領域はおそらく電極の間とその近傍の高電界空間です。周囲の環境にはさまざまな可能性があります。
- ページの外側に長く伸びた電極があって、電気的な接続からかなり離れた断面を見ているとします。この場合、電極の周囲には大きな自由空間があり、電位は大きな距離で接地電位に近づきます。この場合は、比較的粗い解像度で解析領域を拡大し、境界全体にわたって固定電位条件φ=0.0を設定することができるでしょう。この選択により、ノイマン境界が近くにあることによる曲げ効果を排除することができます。妥当な設定であれば、解析領域の正確な大きさは、関心領域の電場にほとんど影響を与えないでしょう。
- 仮に、計算領域に含めないことを選択した、延長された接続構造があるとします。解析領域の上の構造は上部電極の電位にあり、下の構造は下部電極の電位にあるとします。そうすると、電極から遠く離れた場所には、ほぼ均一な垂直電場が存在することになります。この場合は、右図のように上下の境界で固定電位を設定します。また、左右のノイマン境界の影響を減らすために、水平方向の解析領域サイズを大きくすることもできます。
このように、それぞれの解析内容の境界条件を考え、それに合わせて設定を考えなければなりません。このことは一部のユーザーを「どうしてプログラムが解決してくれないんだ?」と憤慨させます。
大事なことは、物理的なシステムを数学的に表現しようとするときはいつでも、すでに計算を制限することを決定しているということです。例えば、アイオワ州ダベンポートの畑に転がっているビール缶は、解析結果にゼロではない(小さいとはいえ)影響を与えるでしょう。それを含めるのか?要するに、コンピュータ・シミュレーションとして、そのようなもの(ある場所で起こりうるすべての影響を含む完璧な解)は存在しないということです。それぞれの数値解は、ユーザーによる様々なフィルタリングの決定を反映しています。










