電極のエッジは、有限要素法計算の落とし穴です。私たちは、プロット上で見栄えのする鮮明なエッジを求める傾向があります。しかし、エッジが計算結果の精度に寄与しない場合、電場計算においてどの程度労力を使うかが問題です。
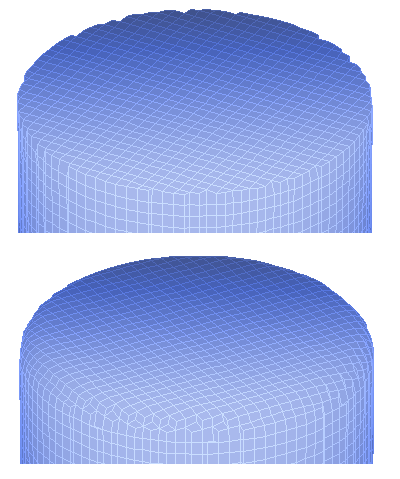
図1 MetaMeshの解像度、シャープエッジとフィレットエッジ。
図1の一番上の例は、MetaMeshで生成した円柱の3次元メッシュです。湾曲した側面は理想に近いですが、側面と上面が接する鋭利なエッジについては、コードによって多少の妥協がなされています。その結果、選択された要素サイズと一致する最適なフィッティングをしています。より小さな要素を使用したり、節点を円形の境界に強制的に近づける(エッジフィット)ことで、エッジの外観を改善することは可能です。しかし2つの欠点があります: 1)計算時間が大幅に長くなる、2)要素の歪みが発生する可能性が高くなる。重要なのは、その欠点を相殺するほどの大きなメリットがあるかどうかです。
ポアソン方程式の性質は、ある体積における静電ポテンシャルの変化を可能な限り滑らかにしようとするものです。鋭い電極の端では、等電位線が急に曲がる必要があり、実質的に無限の局所電場を意味します。このような場はありえないので、自然界のすべてのエッジには半径があります(ただし、小さすぎて見えないかもしれません)。エッジの半径が小さいと、大きな(しかし有限の)電界が得られます。

図2 MetaMeshの解像度とシャープエッジ、フィレットエッジ 電極の先端付近の電界の大きさ。
数値計算では、この要素が空間分解能の限界を決定します。周囲の要素より小さい構造の近くでは、局所的な場の値は妥当ではありません。図2の一番左の場合は、要素サイズよりもはるかに小さな半径を持つ電極エッジ付近の静電場を示しています(色は要素内の平均電界を表しています)。電極点への補間は、|E|に大きな、しかし実質的に意味のない値を与えることになります。要素サイズを小さくすると(真ん中のケースのように)、端から1つ以上離れた位置での電界分布は改善されますが、電極面では単に|E|に異なる意味のない値を与えてしまいます。3つ目のケースは、電極の表面電界を求めるためのより良い方法です。この場合、先端はいくつかの要素にまたがる妥当な曲率半径で表されます。この場合、表面上のすべての位置で、電界の補間により正確な|E|値を得ることができます。
数値コードを無理やり自分の思い通りにしようとするとき、そのコードは何かを伝えようとしていることが多いのです。この例では、MetaMeshは私が高電圧システムで鋭いエッジを使用していることに腹を立てていました。そこで、円柱のエッジに半径をつけると(最初の図の2番目のケース)、コードはほっと一息ついて、自分の仕事を進め、うまく収まるようになりました。
最後に、静電場計算ではすべての部品に半径をつけなければならないと言っているのではないことを強調しておきます。電極表面が対象体積から取り除かれ(ビームラインなど)、電極表面の正確な電界レベルを気にしないのであれば、重要な領域では鋭いエッジは解の精度にほとんど影響を与えません。










